Call-Optionen – Alles zur garantierten Wette auf einen Preisanstieg im Ratgeber.

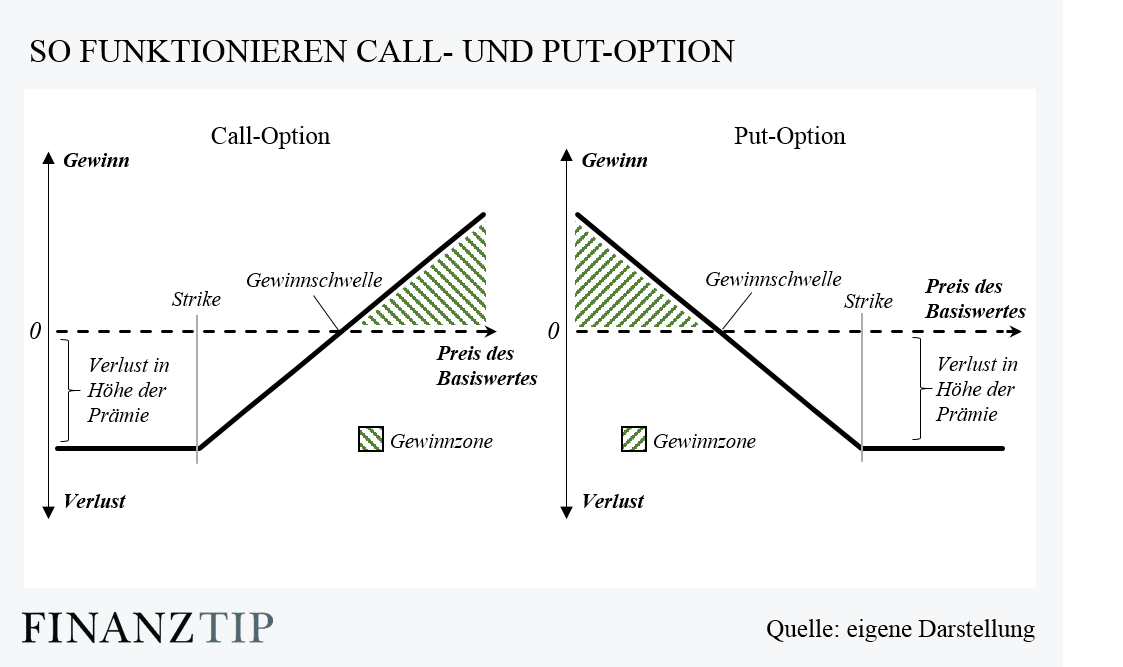
Bei dem Erwerb einer Option hat der Investor die Möglichkeit diese innerhalb eines bestimmten Zeitraums zu einem definierten Preis in vereinbarter Menge zu kaufen. Der Käufer zahlt bei dem Abschluss des Vertrages den sogenannten Optionspreis, welcher die Prämie des Abschlusses der Transaktion darstellt. Nach dem Vertragsabschluss besteht für den Investor die Möglichkeit, die Option an eine andere Person zu verkaufen. Kommt es nicht zu der Ausübung einer Option innerhalb des festgelegten Zeitraums, verfällt diese. In der Regel kommt es zu einem Kauf der betreffenden Option, wenn der Kurs dieser innerhalb der definierten Frist steigt beziehungsweise der Gewinn durch den Kursanstieg unter der Berücksichtigung der Prämie der Option vorhanden ist. Macht ein Käufer von dieser Möglichkeit gebrauch, nutzt dieser die Call-Option. Eine Call-Option bezeichnet deshalb eine garantierte Wette auf einen Preisanstieg.

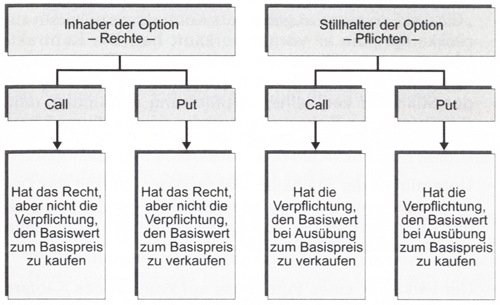
Die Call-Option als Hebelwerkzeug

Die Opportunität eine Call-Option auszuüben bietet dem Investor ein wirksames Werkzeug zur Erzielung einer starken Hebelwirkung. Diese wird dadurch erzielt, dass ein zukünftiger Anstieg des Wertes in Relation zu dem Bezugswert vorhergesehen wird. Durch die Inanspruchnahme der Call-Option kann der Investor eine große Anzahl an Einheiten eines Bezugswertes kontrollieren. Vorteilhaft ist, dass der Käufer nur einen gewissen prozentualen Anteil an Kapital hierfür benötigt, wodurch der Hebeleffekt erreicht wird.

Die Intensität des Hebeleffekts kann individuell auf den Investor abgestimmt werden. Im Rahmen des Hebeleffekts ist die Kennzahl Delta von großer Wichtigkeit. Durch diese kann das Verhältnis des Bezugswerts zum Preis aufgezeigt werden. Delta definiert sich aus der Relation des Bezugswerts und dem Strike-Preis. Als Grundsatz gilt, dass bei einem Steigen ins Geld der Call-Option auch Delta zunimmt. Notiert die Call-Option am Geld, entspricht der Bezugswert meist dem Strike-Preis. Der für eine Call-Option typische vorteilhafte Aspekt sorgt dafür, dass sich mit dem Auslaufen des Preises des Bezugswerts aus dem Geld die Kennzahl Delta senkt und deshalb die Hebeloption der gegen den Investor gerichteten Spekulation.

Der theoretische Wert einer Call-Option

Mithilfe des theoretischen Werts von einem Optionsschein wird angezeigt, wie hoch der Preis der Option sein sollte. Dieser Wert wird durch die Faktoren Bezugspreis, Laufzeit, aktuellee Kurs und Optionspreis gebildet. In der Regel ist der theoretische Wert einer Call-Option mit einer sichtbaren Differenz im größeren oder kleineren Rahmen in Bezug auf den tatsächlichen Wert einer Option ausgestattet. Der theoretische Wert einer Option wird auf dem Finanzmarkt auch mit dem inneren Wert auf eine Stufe gestellt.

Der theoretische Wert einer Option entspricht im täglichen Geschäft mit Optionen nur in den wenigsten Fällen dem gegenwärtigen Preis einer Option. Als Grund hierfür ist der Zeitwert sowie die aktuelle Nachfrage und das Angebot am Markt zu nennen. Durch die Bestimmung des theoretischen Werts einer Option kann der Investor zudem erkennen, ob der auf dem Markt befindliche Optionsschein günstig oder weniger günstig angeboten wird. Beträgt der theoretische Wert einer Option mehr als der aktuelle Marktpreis einer Option, ist das Angebot günstig. Im Gegensatz hierzu ist ein unter dem Wert der gegenwärtig notierenden Option liegende theoretische Wert ein Anzeichen dafür, dass die Option teuer ist.

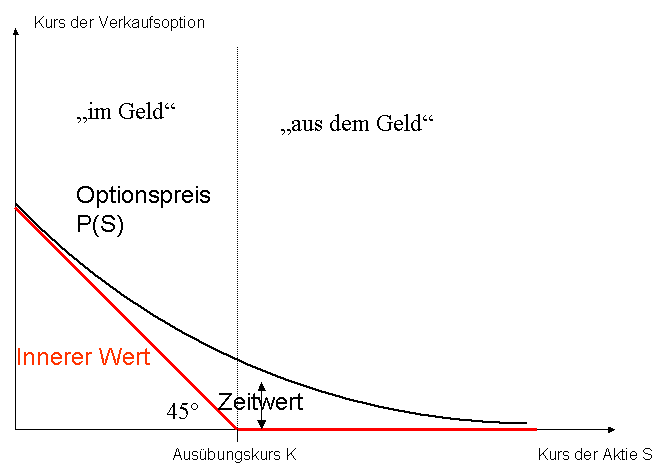
Der innere Wert – der theoretische Wert einer Option

Der innere Wert wird häufig auch als fairer Preis benannt. Dieser ist von folgenden Faktoren abhängig:

– der Volatilität

– der Restlaufzeit

– der Dividende

– dem Zinssatz

Die Ermittlung des theoretischen Preises einer Call-Option kann durch das Ansehen des Rückzahlungstermins einer endfälligen Anleihe erfolgen. Dies bedeutet, dass der innere Wert von dem Bezugswert der Option sowie dem Kurs des Bezugswerts abhängt. Der innere Werte ist bei einem Call-Optionsschein immer dann präsent, wenn dieser einen Profit erwirtschaftet. Besitzt der Optionsschein beispielsweise einen Bezugswert von 50 Euro, ist der innere Wert vorhanden, wenn der Kurs der Option mehr als 50 Euro beträgt. Im Vergleich hierzu besitzt eine Put-Option einen inneren Wert, wenn die Option unter 50 Euro notiert. In allen weiteren Fällen beträgt der innere Wert genau null. Dies liegt daran, dass eine Option nicht in den negativen Bereich wandern kann.

Als Formel für den inneren/theoretischen Wert einer Call-Option gilt deshalb:

Innerer Wert = (Kurs des Bezugswerts – Bezugspreis) * Bezugsverhältnis

Die Rentabilität einer Call-Option

Im Rahmen einer Call-Option kann diese im Geld, am Geld und aus dem Geld sein. Diese Bezeichnungen geben Aufschluss darüber, ob eine Option lohnenswert ist oder nicht. Notiert ein Optionsschein im Geld bedeutet dies bei der Call-Option, dass der Ausübungspreis unter jenem des Spotpreises von dem Bezugswert liegt. Dies heißt, dass eine Call-Option im Geld eine lohnenswerte Investition darstellt. Eine alternative Bezeichnung für dieses Geschehnis ist „in the money“. Ist der Ausübungspreis ebenso hoch wie der Spotpreis eines Bezugswerts, handelt es sich bei der Call-Option um jene am Geld. Synonym hierfür kann auch die Bezeichnung „at the money“ genutzt werden.

Befindet sich bei der Call-Option der Ausübungspreis oberhalb des Spotpreises eines Bezugswerts, ist der Optionsschein aus dem Geld. Die Call-Option ist somit „out of the money“ und für den Investor nicht rentabel.

Bei der Betrachtung von amerikanischen und europäischen Optionen gibt es jedoch einen großen Unterschied bezüglich des inneren Werts. Die europäische Option ist durch das Verbot eines vorzeitigen Optionskaufs ausgestattet, was bedeutet, dass der Investor nach dem Ablaufen der Frist einer Option einen Kauf erwirken kann. Bei einer amerikanischen Option können diese jedoch vorzeitig erworben werden. Dies hat zur Folge, dass die amerikanischen Optionen einen inneren Wert von maximaler Höhe des theoretischen Werts haben. Die europäische Variante ermöglicht es jedoch, dass der innere Wert den theoretischen Wert übersteigen kann.

Die detaillierte Bestimmung des theoretischen Werts – das „Black-Scholes-Modell“

Vor über dreißig Jahren herrschte auf dem Finanzmarkt eine große Unsicherheit bezüglich der Bewertung von Optionen. Hierdurch wurden große Differenzen in Kursen erzeugt, die hinderlich für einen Handel auf dem Geldmarkt gewesen sind. Mithilfe des „Black-Scholes-Modells“ konnte zum ersten Mal der faire Preis einer Option mit Einschränkungen bestimmt werden. Das damals erschaffene Referenz-Modell wird noch heute trotz der Tatsache angewandt, dass die damit verbundenen Annahmen in der praktischen Anwendung nicht immer präsent sind.

Die europäischen Optionen können mithilfe des „Black-Scholes-Modells“ bewertet werden. Hierzu wird ein Portfolio aus einem beliebigen Anteil an Aktien und einer Option geschaffen. Dieses soll ermöglichen, dass bei einem Verlust beziehungsweise Gewinn einer einzelnen Aktie aufgrund einer Kursänderung der unerwünschte Effekt durch die Option ausgeglichen wird. Bei einem klassisch verteilten Zinssatz und einer Rendite ohne Ausfallrisiko zeigt sich bei gleichbleibenden Schwankungen, dass das Portfolio über einen sehr kleinen Zeitraum ohne Risiko ist. Der Wert ist deshalb aufgrund der Nutzung von Preisunterschieden mit dem Zinssatz ohne Ausfallrisiko zur Verzinsung zu bringen. Hieraus entsteht die folgende Formel:

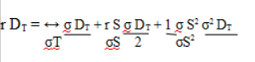
σ = Standardabweichung

r = Zinssatz ohne Ausfallrisiko (konstant)

D_T = Preis der Obligation mit einer restlichen Laufzeit

T = restliche Laufzeit

S = Preis von der Aktie

Aufgrund der Tatsache, dass der Wert der jeweiligen Option am Tag des Verfalls definiert ist, ergibt sich für die Berechnung der Call-Option die folgende Gleichung:

P = Xe^-rT N (↔ d₂) ↔ S N (↔ d₁)

X = Ausübungspreis

P = Preis der Call-Option

N = kum. Funktion der Normalverteilung

Das „Black-Scholes-Modell“ und dessen Betrachtung

Möchte ein Investor ein Portfolio zusammenstellen, besteht die Möglichkeit zum Beispiel halbe Teile von Wertpapieren in diesem zu verzeichnen. Dies basiert auf dem Grundgedanken der Teilbarkeit von Wertpapieren, welcher dazu führt, dass eine bestimmte Anzahl an Optionen diese Entgleisung minimiert. Der Blankoverkauf von Wertpapier ist in Deutschland durchführbar, wenn diese auf der Basis des Ausleihens geschieht. Positiv zu erwähnen sind hierbei die niedrigen Leihkosten des jeweiligen Wertpapiers. Bei amerikanischen Trades fallen keine Leihkosten an. Dieses Szenario ist bei Long Positions sowie Optionen mit einer längeren restlichen Laufzeit jedoch nicht anzutreffen. Grundvoraussetzung für diese Theorie ist ein stetiger Handel.

Da in der Praxis kein stetiger Handel gewährleistet werden kann, können Probleme auftreten, welche jedoch durch tradebasierende Schwankungen des Kurses limitiert werden. Damit diese Problematik umgangen werden kann, sollte bei dem Hinzuziehen des „Black-Scholes-Modells“ die Einheit „Handelstage“ genutzt werden. Bei etwaigen Übernahmen von Wertpapieren auf dem Markt kommt es zu keiner Berücksichtigung dieser im Konzept von Scholes und Black. Dies führt zu der Annahme eines stetigen Zinses, welcher sich somit nicht an Kursen oder Laufzeiten orientiert. Zudem basiert dieses Model auf der Grundlage der sich gleichenden Haben- und Sollzinsen sowie einer Zinsstrukturkurve mit geringer Steigung. Mithilfe des Zinses der Nullkuponanleihen kann ein passender Zinssatz gefunden werden, welcher eine deckungsgleiche restliche Laufzeit wie eine Option hat.

Die Schwankungen auf dem Markt werden von dem „Black-Scholes-Modell“ nicht berücksichtigt. Zur Errechnung des Preises einer Option werden Schwankungen jedoch benötigt, was dazu führt, dass eine große Unbestimmtheit entsteht. Zur Bewertung des Wertes von Optionen ist eine wahrscheinliche Verteilung jedoch essenziell. Ein großer Vorteil des „Black-Scholes-Modells“ im Vergleich zu anderen Modellen zur Berechnung des Wertes einer Call-Option ist dessen einfache Anwendbarkeit sowie Abänderbarkeit. Deshalb wird das nicht der Realität gleichende Modell noch heute bei der Werteberechnung der Call-Option eingesetzt.

Die Zinssatz-Optionen und der Wert der Call-Optionen

Die Zinssatz-Optionen können in zwei Bereiche geteilt werden. In jenen Bereichen zeigen sich die Futures-Optionen sowie die physischen Optionen. Diese Art von Optionen kann durch das Berücksichtigen der Prämie beziehungsweise Kosten bewertet werden. Hierbei wird der Zeitwert sowie der intrinsische Wert/innere Wert berücksichtigt.

Der Zeitwert und dessen Berechnung

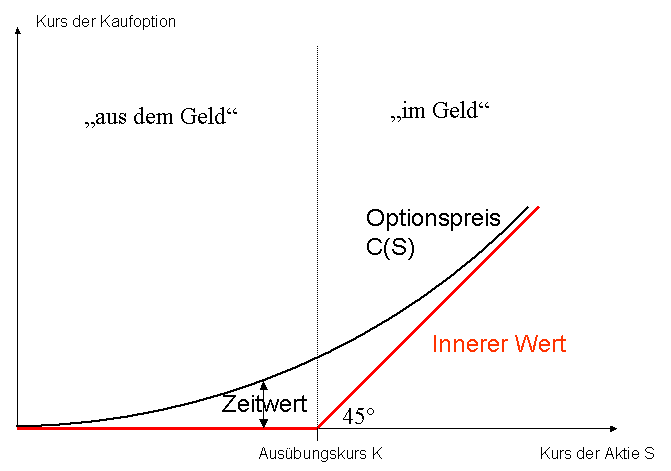
Da der Wert eines Optionsscheins nicht alleine durch den inneren Wert definiert werden kann, wird der Zeitwert zur Hilfe geholt. Dieser Wert wird konstant neu am Markt bestimmt. Der Zeitwert gibt hierbei Aufschluss über jenen Anteil eines Optionspreises, welcher nicht mithilfe des inneren Wertes gedeckt wird. Jene Optionsscheine, welche aus dem Geld gelistet werden, sind für einen Investor nicht gänzlich wertlos, trotz der Tatsache, dass der Kurs eines Wertpapiers unterhalb des Ausübungspreises rangiert. Der betreffende Schein verfügt jedoch über einen inneren Wert in Höhe von null. Da der Zeitwert jedoch berücksichtigt wird, erhält der Investor den Schein der Option nicht ohne Kosten. Der Zeitwert lässt sich somit wie folgt errechnen:

Zeitwert = Preis des Optionsscheins – innerer Wert

Die beeinflussenden Faktoren des Zeitwertes sind somit:

– der Zinssatz

– die restliche Laufzeit

– die Schwankungen des Bezugswerts

– der Kurs des Bezugswerts

– die Dividende

Hierdurch wird verdeutlicht, dass der Zeitwert auf Dauer gesehen an Wert einbüßt. Dies bedeutet, dass mit der Annäherung des Endes der Laufzeit der Zeitwert abnimmt. Zudem bedeutet eine Näherung an das Ende der Laufzeit eine Minimierung der Möglichkeit der Ausbildung eines günstigen Underlyings. Da aufgrund dessen die Wahrscheinlichkeit eines Gewinns sinkt, besitzen die Optionsscheine mit niedrigerer Laufzeit bei einem konstanten Ausführungspreis und Bezugswert meist einen geringeren Zeitwert im Vergleich zu jenen mit gesteigerter Laufzeit. In Bezug auf eine Call-Option wird deshalb gezeigt, dass die Abnahme des Zeitwerts lediglich durch eine Steigerung des Kurses ermöglicht werden kann. Bei einer Put-Option muss es sich deshalb um einen Kursrückgang handeln, damit der Zeitwert zur Abnahme kommt. Ist das Ende der Laufzeit erreicht, beträgt der Zeitwert null. Dies bedeutet, dass eine Option am Ende der Laufzeit lediglich durch den inneren Wert definiert wird. Hierdurch wird verdeutlicht, dass das Verkaufen von einer Option für den Investor bevor das Ende der Laufzeit erreicht ist, in der Regel vorteilhafter ist, als das Recht des Optionsscheins in Anspruch zu nehmen. Dies liegt daran, dass der Zeitwert in diesem Fall berücksichtigt werden kann und nicht am Ende der Laufzeit eliminiert wird.

Wird zum Beispiel eine Call-Option für zehn Euro erworben, deren innerer Wert zum Zeitpunkt des Erwerbs vier Euro beträgt, ist der Zeitwert sechs Euro. Des Weiteren wird der Kurs der Option am Verfallstag mit 54 Euro angegeben. Da der Kurs am Tag des Verfalls keinen Zeitwert hat, ist der Preis der Option mit dem inneren Wert anzugeben, welcher zu diesem Zeitpunkt fünf Euro betrug. Dies würde für den Investor bedeuten, dass dieser eine Call-Option für zehn Euro gekauft hätte, welche am Tag des Verfalls lediglich für fünf Euro hätte verkauft werden können. Somit hätte der Investor einen Verlust von 50 Prozent erlitten, trotz der Tatsache, dass die Anlage einen Euro Gewinn pro Stück erwirtschaftet hat.

Bei der Investition in Optionen sollte der Anleger wissen, dass der Verlust des Zeitwerts konstant geschieht, jedoch innerhalb der letzten Monate eine prozentuale Zunahme des stetigen Wachstums verzeichnet. Deshalb sollten Investoren keine Optionen erwerben, welche eine kurze Laufzeit besitzen und aus dem Geld gehen, da dies zu einem totalen Verlust führen kann.