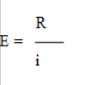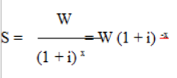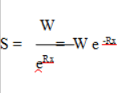Verzinsung kontinuierlichen Diskontierung – Alle Formeln und Ihre Anwendung!

Zuletzt aktualisiert & geprüft: 27.10.2020

Inhaltsverzeichnis Anzeigen

Der Zweck der Verzinsung einer Diskontierung

Werden zukünftig fällige Zahlungen betrachtet, so zeigt sich, dass der Wert dieser meist niedriger als die Höhe der Zahlung ist. Dies liegt daran, dass die Teilnehmer auf dem Markt aktiv handeln möchten. Der betreffende Betrag wird als nutzvoll angesehen, wenn dieser frühzeitig verwendet werden kann. Der Wert zur gegenwärtigen Zeit, welcher paritätisch zu einer Zahlung zu einem späteren Zeitpunkt ist, ist kontinuierlich kleiner als die betreffende Zahlung. Der Anleger möchte für eine geforderte Zahlung zum Zeitpunkt t von Y Euro zum gegenwärtigen Zeitpunkt nicht mehr bezahlen als Y. Mithilfe der Diskontierung kann der Anleger die Beziehung dieser zum Zinssatz wie folgt erkennen:

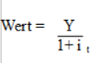
Der Zinssatz i _t kann auf eine beliebige Periode wie ein Jahr bezogen werden, wodurch i _t = i ₁wäre. Mithilfe des Geschehens am Markt kann die Zahlung in der Zukunft gewertet werden, wodurch die Option besteht, den Zinssatz ermitteln zu können. Auf der Basis des errechneten Zinses kann eine gewünschte Zahlung bewertet werden.

Jetzt zum Testsieger eToro!74% der Konten von Kleinanlegern verlieren Geld beim Handel mit CFDs bei diesem Anbieter. Sie sollten sich überlegen, ob Sie das hohe Risiko, Ihr Geld zu verlieren, eingehen können. Krypto-Investitionen werden von eToro (Europe) Ltd. angeboten und die Verwahrung wird von eToro Germany GmbH durchgeführt. Ihr Kapital ist gefährdet.

Die zwischenjährlichen Zinszahlungen [Verzinsung]

In der Regel basiert die Berechnung der Zinsen auf der jährlichen Annahme. Nachfolgend kann der Investor erkennen, wie zwischenjährliche Zinszahlungen zu berücksichtigen sind. Hierbei können die Intervalle wie halbjährlich, monatlich oder vierteljährlich als Grundlage gesehen werden. Es besteht zudem die Möglichkeit tagegenau zu rechnen, was jedoch in der Praxis seltener geschieht. Damit die gewünschte Periode des Zinses ermittelt werden kann, wird das Jahr in Intervalle unterteilt, welche kumuliert ein Jahr betragen.

Die Perioden zwischenjährlichen Zinsen werden hierbei mit der Kennzahl m versehen. Wird nun beispielsweise die Einheit der Periode von einem Tag gewählt, beträgt m 365 oder 360. Dies ergibt sich aus der Tatsache, dass im Rahmen einer Anlage die Zeiträume dieser nicht genau ein Jahr betragen müssen. Üblicherweise werden die Tage mithilfe von x/y angegeben. Hierbei bezeichnet x die Option der Zählung von den Tagen innerhalb von zwei Zeitpunkten der Zinszahlung und y die Gesamtheit der Tage eines Jahres. Für den Ertrag der Zinsen ergibt sich deshalb die Gleichung:

Bei der auf den Tag genauen Zinsmethode werden alle Tage der Anlage in die Relation mit der Anzahl aller möglichen Anlagetage des Jahres gesetzt. Diese Variante der Errechnung wird meist auf den europäischen Finanzmärkten genutzt. Auch die Variante 30/360 ist bei Anlegern beliebt. Dabei wird jeder ganze Monat immer mit 30 Tagen angesetzt. Dies bedeutet im Umkehrschluss, dass ein Jahr aus 360 Tagen besteht.

Fällt die Wahl der Periode auf die monategenau Betrachtung, beläuft sich der Wert von m auf zwölf. Der zwischenjährliche Zins kann mit z gekennzeichnet werden, wohingegen die Laufzeit der gewählten Anlage mit N benannt wird.

Die Errechnung der Zinsen mit geringeren Laufzeiten als einem Jahr kann auf verschiedenen Wegen durchgeführt werden.

Variante I – die zwischenjährlichen Zinssätze [Verzinsung]

Eine Variante ist es die bereits existierenden Gleichungen der jährlichen Zinszahlungen für jene der zwischenjährlichen Zinszahlungen zu nutzen. Die Formel wird dahin gehend abgeändert, dass nicht das Jahr als Basis genutzt wird, sondern die gewählte Periode des Zinses. Damit N, die Laufzeit, errechnet werden kann, muss der Anleger die nachfolgende Rechnung ausführen:

N = m * n

Hat eine Anlage des Kapitals zum Beispiel eine Laufzeit von vier Jahren und nutzt die periodische Betrachtung in Quartalen, kann die Laufzeit mit N = 4 * n = 16 Quartalen ermittelt werden. Durch das Nutzen dieser Gleichung ist es dem Investor möglich die Formeln von den jährlichen Verzinsungen zu beanspruchen. Jedoch muss der Anwender der Gleichung beachten, dass die Kennzahl n beziehungsweise N in der Basisgleichung anstelle von i, dem jährlichen Zins, der zwischenjährliche Zins z tritt. Deshalb kann die folgende Formel für die zwischenjährliche Verzinsung genutzt werden, um K _N, das Endkapital, zu errechnen:
K _N = K ₀ · (1 + N * z)
Damit der Anleger das Startkapital K ₀ von dem der Laufzeit N oder dem Zins z berechnen kann, muss eine Umstellung der betrachteten Formel erfolgen, woraus sich ergibt, dass bei der zwischenjährlichen Verzinsung die jährliche Verzinsung des Zinseszins genutzt werden kann. Hierbei muss jedoch die vorausgehende Ersetzung beachtet werden. K _N, das Endkapital, kann demnach wie folgt ermittelt werden:
K _N = K ₀ · (1 + z)[N]

Variante II – die zwischenjährlichen Zinssätze [Verzinsung]

Die nächste für den Investor nutzbare Möglichkeit zur Berechnung der zwischenjährlichen Zinsen ist es die Messung der Laufzeit in Jahren auszuführen und die zwischenjährlich entstehenden Zinsen zu adjustieren. Wird die Laufzeit somit in Wochen, Monaten oder Tagen angegeben, muss diese in Jahren wiedergegeben werden. Wird eine Laufzeit von sechs Monaten betrachtet, beträgt diese genau 0,5 Jahre. Analog hierzu sind die zwischenjährlichen Zinssätze in Zinssätze per anno umzurechnen. Der Anleger muss hierbei jedoch bedenken, dass grundsätzlich die Option besteht diese Umrechnung auf der Basis der Zinseszinsen oder der einfachen Zinsen auszuführen. Hierbei wird somit entweder der Nominalzins oder der konforme Zins genutzt. Die Kennzahl j steht hierbei für den zwischenjährlichen Zins sowie den relativen Zins. Der Nominalzinssatz wird mit i bezeichnet und benennt den relativen Zins bei einer Verzinsung in einfacher Form in Bezug auf ein einziges Jahr. Somit ergibt sich:

i = z * m

Bei der Betrachtung von i*, dem konformen Zins, kann folgende Formel definiert werden:

i* = (1 + z) [m]- 1

Vergleicht der Anleger beide Möglichkeiten der Errechnung der zwischenjährigen Zinsen zeigt sich, dass beide Methoden zu dem gleichen Ergebnis führen.

Die Zinskurve und der Diskontfaktor

Durch das Aufzeigen des Diskontfaktors kann der Anleger erfahren, wie sich eine zukünftig fällige Zahlung auf den gegenwärtigen Preis einer Anlage auswirkt. Dies wird mithilfe der Strukturkurve des Zinses aufgezeigt. Auf dem Kapitalmarkt gibt es Zinsen für alle möglichen Fristigkeiten einer Anlage. Hieraus ergibt sich der Zinssatz i _1/t, i ₁, i ₂, …, i ₁₅, …, welcher unterschiedliche Möglichkeit der Bindung aufzeigt. Aufgrund dieser variablen Fristigkeiten ist auch die Kurve des Zinses in unterschiedlichen Ausprägungen vorhanden. In der Regel ist die Zinskurve nicht flach.

Aus Beobachtungen geht jedoch hervor, dass die Kurve des Zinses eben ist und die Differenzen zwischen den Zinsen unterschiedlicher Fristen niedrig sind. Dies liegt daran, dass die Zinsen für eine definierte Laufzeit abhängig sind. Im Rahmen einer Anlage gibt es die Option diese zu ersetzen, was den Investoren bekannt ist. Aus diesem Grund können sich die Bedingungen einer Anlage innerhalb einer betrachteten Frist ähnlich sein. Die Bildung eines Kurses ist somit von der Konzipierung anderer Kurse abhängig. Die Handlungen auf einem Finanzmarkt sind somit miteinander verknüpft. Investoren, welche für circa drei Jahre Geld auf dem Markt anlegen möchten und eine Anleihe mit einer restlichen Laufzeit von drei Jahren zu kostspielig erachten, wählen eine weniger kostspielig erscheinende Anlage mit einer Laufzeit von vier Jahren. Der Investor plant somit diese Anleihe nach drei Jahren zum Verkauf auf dem Markt anzubieten. Es besteht jedoch auch die Option eine Anleihe mit einer restlichen Laufzeit von lediglich zwei Jahren zu erwerben und diese am Laufzeitende mit dem erwirtschafteten Geldbetrag für ein Jahr anzulegen.

Damit der Investor nicht dauerhaft mit der Potenzierung arbeiten muss, kann dieser eine Diskontierung vornehmen. Diese zeigt dem Anleger den Zusammenhang zwischen einer zukünftigen Zahlung und deren Beziehung zum aktuellen Preis auf dem Markt. Der Diskontfaktor ist mithilfe der nachfolgenden Formel unkompliziert zu ermitteln:

Somit bezeichnet D_tden Faktor des Diskonts den Preis des Geldes, welcher in t Jahren gezahlt werden muss. Deshalb besitzt die Menge X des Geldes in t Jahren den Marktpreis D _t* X.

Erfolgreich den Ertragswert einer Investition ermitteln

Mithilfe der Integralrechnung besteht die Möglichkeit die kontinuierliche Diskontierung zu ermitteln. Durch die Ermittlung dieser kann der Anleger den Ertragswert einer Investition definieren und erhält somit die Grundlage des erfolgreichen Anlegens. Bei der Betrachtung einer Anlage, deren Kosten der Anschaffung in Höhe von P₀ = P anfallen, werden über eine bestimmte Zeitdauer von X Jahren konstante Erträge (netto) R erwartet.

Deshalb gilt der folgende Zusammenhang:

x = 1,…., X

R_x = R
Damit der Investierende genau abschätzen kann, ob eine Anlage lohnenswert ist, muss dieser die Kosten der Anschaffung in Relation zu den innerhalb eines Zeitraums anfallenden Erträgen (netto) setzen. Um dies zu ermöglichen werden alle in der Zukunft erwarteten Erträge (netto) mit einem passenden Zinsfuß der Kalkulation i auf den momentanen Zeitpunkt diskontiert. Im Anschluss daran werden die hieraus gewonnenen Werte zu einer Ertragssumme kumuliert. Der Barwert innerhalb des Intervalls x des erwarteten Nettoertrags R_x kann deshalb von dem Anleger mit der folgenden Formel bestimmt werden:

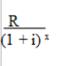
Werden nun alle Intervalle betrachtet kann der Ertragswert mit der nachfolgenden Gleichung ermittelt werden:

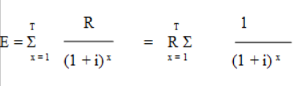
Die zwischenjährliche Diskontierung

Bei einer zwischenjährlichen Diskontierung beziehungsweise jener in folgenden Formen:

– halbjährlich

– vierteljährlich

– täglich

wird der Ertrag (netto) in diesen Intervallen diskontiert. Hierbei ergibt sich ein Jahr aus mehreren Perioden n mit der Dauer von D x = 1/n. Hiermit kann der Anleger den sogenannten Faktor zur Abzinsung für zwischenjährliche Perioden ermitteln. Errechnet werden kann dieser folgendermaßen:

berechnen lässt.

Bei Anlagen mit längerer beziehungsweise nahezu unendlicher Dauer wie zum Beispiel den dauerhaften Anleihen läuft X gegen unendlich. Hieraus ergibt sich der Grenzwert, welcher jenem der diskreten Abzinsung entspricht:

Nachdem der Investor den Ertragswert errechnet hat, findet dieser heraus, ob eine Anlage lohnenswert ist. Hierbei muss der Ertragswert höher sein als die Kosten der Investition.

Die Diskontierung und das Wachstum

Bei der Abzinsung ist anzumerken, dass diese eine sehr enge Relation zu der Verzinsung besitzt. Wird beispielsweise im Rahmen des Zinseszins der zukünftige Wert W mithilfe eines Startbetrags S gesucht, kann dies bei der Diskontierung zu Problemen führen. Das liegt darin begründet, dass der Vorgang der Abzinsung in die komplett andere Richtung verläuft. Der Anleger hat nun das Ziel den Barwert B zu einem Betrag in der Zukunft W zu errechnen. Dieser Betrag ist jedoch in x Perioden vorhanden.

Im diskreten Fall bedeutet dies, dass der Startbetrag S in x Jahren mit dem Prozentsatz i zu verzinsen ist. Hieraus ergibt sich:

W = S (1 + i) ^x
Anschließend teilt der Anleger durch (1 + i) ^xund erhält somit die Formel zur Diskontierung. Möchte der Investor die Abzinsung ausführen, ist folgende Gleichung anzuwenden:

Aufgrund des Tauschens der Kennzahlen W und S erhielt der Exponent ein negatives Vorzeichen. Deshalb wird nun S gesucht und W ist der gegebene Wert. S lässt sich mithilfe des Diskontierungssatzes, x und W berechnen.

Der Vorgang der Errechnung ist für die kontinuierliche Diskontierung ähnlich. Hierbei sei vorausgesetzt, dass der Startbetrag S innerhalb von x Jahren ein kontinuierliches Wachstum um R (Rate) erzeugt und somit auf Se ^Rxwächst. Hierdurch ergibt sich:
W = Se ^Rx
Damit der Anleger die Formel zu der Diskontierung erhält, muss dieser bei der kontinuierlichen Variante die Gleichung beidseitig durch e^Rxteilen. Nachfolgend kann der Investor die Formel zu der kontinuierlichen Diskontierung erhalten, welche wie folgt lautet:

Bei dieser Variante ist S die gesuchte Zahl, welche sich mithilfe W, x sowie dem Diskontierungssatz in nominaler Form (R) errechnen lässt. Der Ausdruck e^Rx wird auch häufig als Faktor der Diskontierung bezeichnet. Die stetige Rate des Wachstums (- R) ist im Rahmen der Gleichung an S ablesbar. Aufgrund der Annahme, dass die Rate des Wachstums negativ ist, zeigt dies eine Senkung der Rate. Der Investor erhält demnach die Information, dass bei der Diskontierung ein negatives Wachsen möglich ist.